Validate Binary Tree Nodes

Problem Statement

You have n binary tree nodes numbered from 0 to n - 1 where node i has two children leftChild[i] and rightChild[i], return true if and only if all the given nodes form exactly one valid binary tree.

If node i has no left child then leftChild[i] will equal -1, similarly for the right child.

Note that the nodes have no values and that we only use the node numbers in this problem.

Leetcode Link

Example 1:

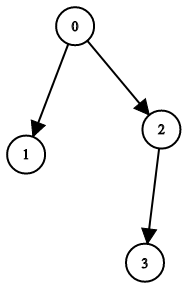
Input: n = 4, leftChild = [1,-1,3,-1], rightChild = [2,-1,-1,-1]
Output: true

Example 2:

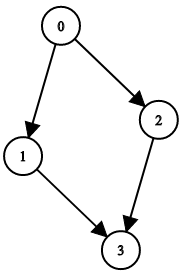
Input: n = 4, leftChild = [1,-1,3,-1], rightChild = [2,3,-1,-1]
Output: false

Example 3:

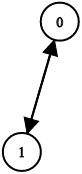
Input: n = 2, leftChild = [1,0], rightChild = [-1,-1]
Output: false

Constraints:

• n == leftChild.length == rightChild.length
• 1 <= n <= 10⁴
• -1 <= leftChild[i], rightChild[i] <= n - 1

Code

Python Code

from collections import deque
class Solution:
    def validateBinaryNodes(self, n, leftChild, rightChild):
        # find the root node, assume root is node(0) by default
        # a node without any parent would be a root node
        # note: if there are multiple root nodes => 2+ trees
        root = 0
        childrenNodes = set(leftChild + rightChild)
        for i in range(n):
            if i not in childrenNodes:
                root = i

        # keep track of visited nodes
        visited = set()
        # queue to keep track of in which order do we need to process nodes
        queue = deque([root])

        while queue:
            node = queue.popleft()
            if node in visited:
                return False

            # mark visited
            visited.add(node)

            # process node
            if leftChild[node] != -1:
                queue.append(leftChild[node])
            if rightChild[node] != -1:
                queue.append(rightChild[node])

        # number of visited nodes == given number of nodes
        # if n != len(visited) => some nodes are unreachable/multiple different trees
        return len(visited) == n