Skip to main content

Number of Ways to Paint N × 3 Grid

Problem Statement​

You have a grid of size n x 3 and you want to paint each cell of the grid with exactly one of the three colors: Red, Yellow, or Green while making sure that no two adjacent cells have the same color (i.e., no two cells that share vertical or horizontal sides have the same color).

Given n the number of rows of the grid, return the number of ways you can paint this grid. As the answer may grow large, the answer must be computed modulo 109 + 7.

Leetcode Link

Example 1:​

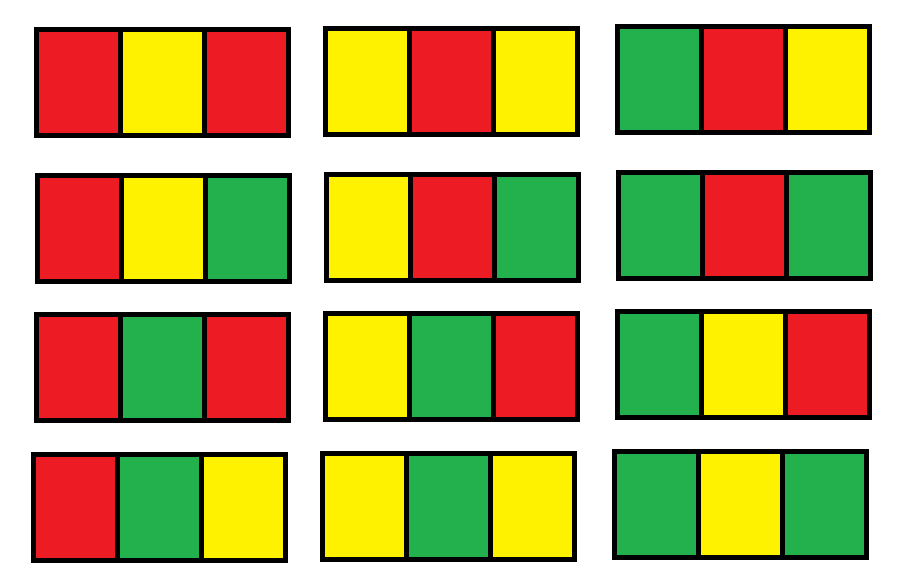
Example

Input: n = 1
Output: 12
Explanation: There are 12 possible way to paint the grid as shown.

Example 2:​

Input: n = 5000
Output: 30228214

Constraints:​

  • n == grid.length
  • 1 <= n <= 5000

Code​

Python Code
class Solution:
    def numOfWays(self, n: int) -> int:
        MOD = 1000000007
        P = ['ryr', 'yry', 'gry', 'ryg', 'yrg', 'grg', 'rgr', 'ygr', 'gyr', 'rgy', 'ygy', 'gyg']
        nei = [[i for i, x in enumerate(P) if all(a != b for a, b in zip(x, p))] for p in P]

        dp = [1] * 12
        for i in range(n - 1):
            dp = [sum(dp[j] for j in nei[i]) % MOD for i in range(12)]
        return sum(dp) % MOD