Wildcard Matching

Problem Statement

Given an m x n integer matrix heightMap representing the height of each unit cell in a 2D elevation map, return the volume of water it can trap after raining.

Leetcode Link

Example 1:

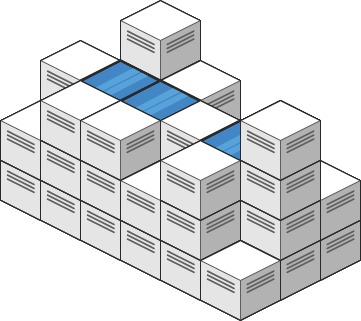
Input: heightMap = [[1,4,3,1,3,2],[3,2,1,3,2,4],[2,3,3,2,3,1]]
Output: 4
Explanation: After the rain, water is trapped between the blocks.
We have two small ponds 1 and 3 units trapped.
The total volume of water trapped is 4.

Example 2:

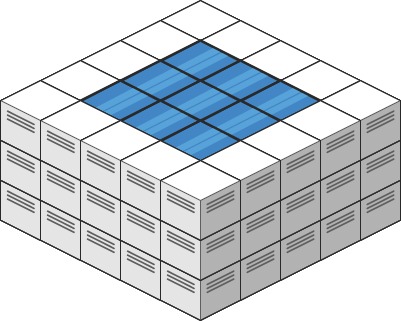
Input: heightMap = [[3,3,3,3,3],[3,2,2,2,3],[3,2,1,2,3],[3,2,2,2,3],[3,3,3,3,3]]
Output: 10

Constraints:

• m == heightMap.length
• n == heightMap[i].length
• 1 <= m, n <= 200
• 0 <= heightMap[i][j] <= 2 * 10⁴

Code

Python Code

class Solution:
    def trapRainWater(self, heightMap: List[List[int]]) -> int:
        if not heightMap or not heightMap[0]:
            return 0


        # Initial
        # Board cells cannot trap the water
        m, n = len(heightMap), len(heightMap[0])
        if m < 3 or n < 3:
            return 0


        # Add Board cells first
        heap = []
        for i in range(m):
            for j in range(n):
                if i == 0 or i == m - 1 or j == 0 or j == n - 1:
                    heapq.heappush(heap, (heightMap[i][j], i, j))
                    heightMap[i][j] = -1


        # Start from level 0
        level, res = 0, 0

        while heap:
            height, x, y = heapq.heappop(heap)
            level = max(height, level)

            for i, j in [(x - 1, y), (x + 1, y), (x, y - 1), (x, y + 1)]:
                if 0 <= i < m and 0 <= j < n and heightMap[i][j] != -1:
                    heapq.heappush(heap, (heightMap[i][j], i, j))

                    # If cell's height smaller than the level, then it can trap the rain water
                    if heightMap[i][j] < level:
                        res += level - heightMap[i][j]

                    # Set the height to -1 if the cell is visited
                    heightMap[i][j] = -1

        return res