Print Binary Tree

Problem Statement

Given the root of a binary tree, construct a 0-indexed m x n string matrix res that represents a formatted layout of the tree. The formatted layout matrix should be constructed using the following rules:

• The height of the tree is height and the number of rows m should be equal to height + 1.
• The number of columns n should be equal to 2^height+1 - 1.
• Place the root node in the middle of the top row (more formally, at location res[0][(n-1)/2]).
• For each node that has been placed in the matrix at position res[r][c], place its left child at res[r+1][c-2^height-r-1] and its right child at res[r+1][c-2^height-r-1].
• Continue this process until all the nodes in the tree have been placed.
• Any empty cells should contain the empty string "".

Return the constructed matrix res.

Leetcode Link

Example 1:

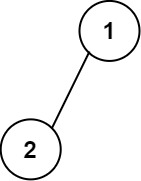
Input: root = [1,2]
Output:
[["","1",""],
 ["2","",""]]

Example 2:

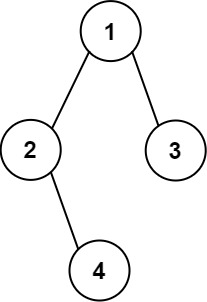
Input: root = [1,2,3,null,4]
Output:
[["","","","1","","",""],
 ["","2","","","","3",""],
 ["","","4","","","",""]]

Constraints:

• The number of nodes in the tree is in the range [1, 2¹⁰].
• -99 <= Node.val <= 99
• The depth of the tree will be in the range [1, 10].

Code

Python Code

import collections

def find_max_depth(node):
    if not node:
        return 0
    max_depth = max(find_max_depth(node.left), find_max_depth(node.right))
    return max_depth + 1

class Solution(object):
    def printTree(self, root):
        """
        :type root: TreeNode
        :rtype: List[List[str]]
        """
        max_depth = find_max_depth(root)

        # build matrix
        matrix_depth = max_depth
        matrix_width = (2**max_depth) - 1
        matrix = [[""] * matrix_width for _ in xrange(matrix_depth)]

        # run level order / breadth first search
        queue = collections.deque()
        queue.append([root, 0, matrix_width - 1, 0]) # node, start, end, level
        while queue:
            node, start, end, level = queue.popleft()
            if not node: continue
            mid = start + (end-start)/2
            matrix[level][mid] = str(node.val)
            queue.append([node.left, start, mid-1, level+1])
            queue.append([node.right, mid+1, end, level+1])
        return matrix