Minimum Path Sum

Problem Statement

Given a m x n grid filled with non-negative numbers, find a path from top left to bottom right, which minimizes the sum of all numbers along its path.

Note: You can only move either down or right at any point in time.

Leetcode Link

Example 1:

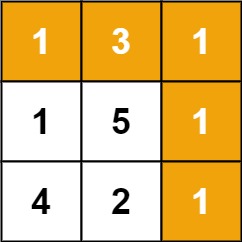
Input: grid = [[1,3,1],[1,5,1],[4,2,1]]
Output: 7
Explanation: Because the path 1 → 3 → 1 → 1 → 1 minimizes the sum.

Example 2:

Input: moves = "LL"
Output: false
Explanation: The robot moves left twice. It ends up two "moves" to the left of the origin. We return false because it is not at the origin at the end of its moves.

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 200
• 0 <= grid[i][j] <= 100

Code

java Code

class Solution {
    public int minPathSum(int[][] grid) {
        for(int i = 1; i < grid.length; i++)
            grid[i][0] += grid[i - 1][0];

        for(int j = 1; j < grid[0].length; j++)
            grid[0][j] += grid[0][j - 1];

        for(int i = 1; i < grid.length; i++) {
            for(int j = 1; j < grid[0].length; j++) {
                grid[i][j] += Math.min(grid[i - 1][j], grid[i][j - 1]);
            }
        }

        //for(int i = 0; i < grid.length; i++)
            //System.out.println(Arrays.toString(grid[i]));

        return grid[grid.length - 1][grid[0].length - 1];
    }
}